https://arxiv.org/abs/2306.11343
Introduction
完全なラベルで学習することがDNNの性能を引き上げる重要な要素だが、プライバシーや機密性、アノテーションコストの高さから個々のインスタンスについてのラベルを詳細には与えることはできず、ある程度のインスタンスグループに対してのラベルのみ与えられる場合がある。
ユーザ情報のプライバシーのため、グループで○○という統計量だったと開示するなど。あとは薬物活性予測でもグループごとにラベルがついたりする。
集合観測=Aggregate Observationによる分類タスク、CFAO(Classification from Aggregate Observation)は必要である。
よくあるのが、Multi-instance Learning。グループ内で○○のラベルを持つデータは少なくとも1つはある、というように。
また、ラベルの割合から学習するLearning from Label Proportionもある。
2つのペアの類似度で学習するClassification from Pairwise Similaritiesもある。
先行研究におけるCFAOは、普遍的な手法は最大尤度推定に基づいていた。だが、それではグループ内ですべてのサンプルで○○の性質を持っていると推定するものであり、リスク一貫性が保証されない(学習を進めても真のLabelで学習したものと同じ収束先にはいかない)。そして対数尤度を使うので、損失関数が限られている。
この論文では、不偏推定量を提案した。
事前知識
CFAO
グループについての統計量からの分類学習を考える。これは以下のように定義される。
- このように各グループが与えられる。
- 与えられはしないが、真のラベルはである。
- 与えられるのは、表現空間にあるAggregate Labelのである。
- Aggregation Labelはある関数で写像される。
- 目標は、を与えられて、正しく各サンプルについて、を予測すること。
具体例としては、
- の場合は、2つのデータが同じか違うか。
- の場合は、大小関係がかどうか。
- の場合、1つでもPositiveはあるか。
- の場合、ラベルの比率がどうなっているか。
- の場合、2つのデータの順位付けかどうか。
そのうえで、グループの中に属しているデータは独立であるという仮定を持つ。
これを踏まえると以下のように、は以下のように計算できる。
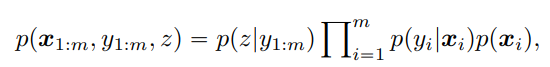
提案手法
不変リスク推定量
不変リスク推定量は以下のようになる。
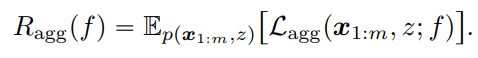
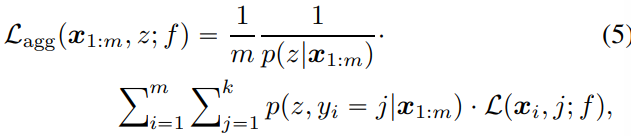
ここでは、
- 各サンプルに対して、考える。真のラベルがだとしたときの損失と、それがとなり、Aggregation Labelもになる条件付確率を乗じる。
- これを各ラベル、各サンプルについて合算する。
- 全部でサンプルあるので、で平均をとる。そして確率は、ラベル条件をなくしたで正則化する。
つまり、なる確率が低いラベルに対しては重みを減らしていくことで、すべてのラベルだった場合の損失を計算している。
これを経験的に最小化すると、以下のようにできる。
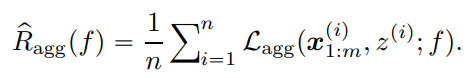
現実的には、どのようにとを推定するのが問題となる。もちろん集約関数によってもそれぞれが違う推定方法をとるだろう。
EMの視点からの分析
を推定したい。
これについて対数尤度を最大化する学習を考える。それをするには隠れ変数のがカギを握る。なので、これはEMアルゴリズムを考えられる。
📄EM Algorithmの解説 のなかのはここではにあたる。
Eステップではと今時点での推定を代入することにあたる。ここでは、のパラメタを固定して、を計算する。
Mステップでは、を最大化する。これは今の推定したに基づいて、においての期待値に相当するを最大化することにあたる。
ここで、右辺はという与えられている変数ともjoint distributionであるでないといけないが、今回の影響はhidden labelののイテレーションにのみ影響し、が成り立つから外している(Ground Truthのラベルからを計算するし)
提案手法の実現
この論文が考えているCFAOは以下のを考える。
- ペアごとの類似性による分
- 3つ組の比較による分類
- 複数インスタンス学習(1つのデータは最低でもXXである)
- ラベルの比率からの学習
類似性や3つ組での学習をすると、最悪識別不能になることがある。情報が少なさすぎて学習が難しいから。なので、近いデータについては近い予測になるというconsistencyはないが、Risk Consistencyだけは保証できる。
そして、識別可能なマッピングも重要である。例えば、学習した3つのクラスがクラス1: 犬、クラス2: 猫、クラス3: 鳥だが、常にこの通りに出力されず、クラス1: 鳥、クラス2: 猫、クラス3: 犬となる可能性もあるということ。
これを解決するために、ハンガリーアルゴリズムという線形割り当て問題を解くためのアルゴリズムで、クラスをマッチさせる。
各CFAOの方法ごとに識別可能性の問題ごとに、推定方法を考える。
ペアごとの類似度
2つのデータが同じクラスに属するか、違うクラスに属するか
この場合は、とは、サンプルに対して識別器の出力したクラスである確率。
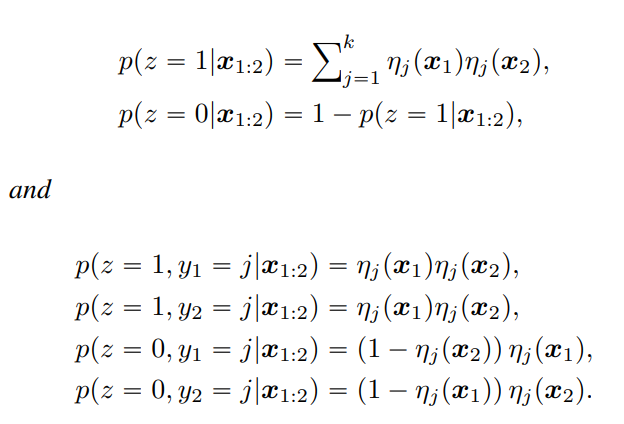
以上のように計算できる。
3つ組の比較
Ground Truthのラベルに対して、かどうか
ここでは、距離をと置いた時の例を示している。
これは以下のようになる。
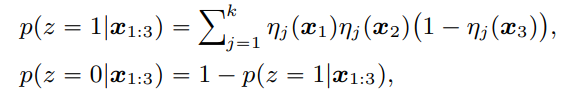
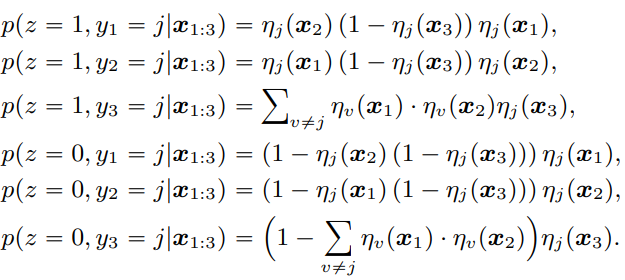
ラベルの割合から学習
与えられるのはではなく、各ラベルのデータの個数のベクトルである。
では、ありうるすべての組み合わせについての走査をしている。
そして具体的なの計算では、番目だけラベルが決まっているということなので、最後にをかけている。
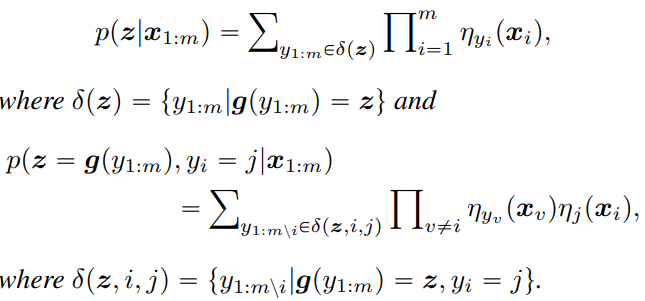
Multi-instance Learning
一連のラベルの中に、1つでもPositiveがあるかどうか
二値分類なので、Pの確率を、Nの確率をとする。
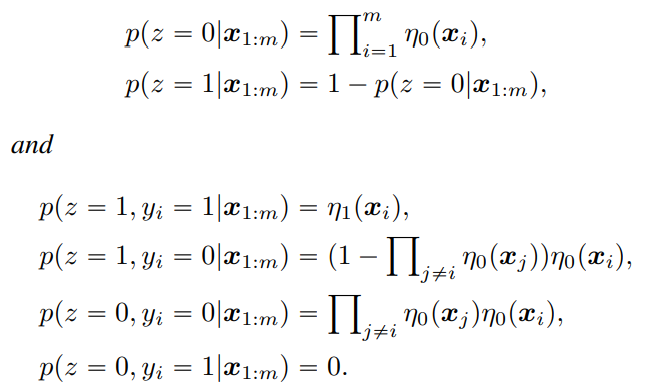
Experiments
- MNIST、Kuzushiji-MNIST、FMNIST、SVHN、CIFAR-10についてそれぞれこれの問題設定で実験した。
- ネットワークはLeNet, DenseNet, MLPなどを使った。
- 損失はCross Entropy。
- 5回ずつ実験した。
結果は少しだけ改善されてた感がある。
